975. Floyd

Given a directed weighted graph. Find a pair of vertices, the shortest distance from one of them to another is maximum among all pairs of vertices.

Input. The first line contains the number of vertices n (1 ≤ n ≤ 100). The next n lines of n numbers describe the weighted matrix. Here -1 means no edges between vertices, and any non-negative number - the presence of an edge of given weight. All elements on the main diagonal are always zero.

Output. Print the desired maximum shortest distance.

Sample input	Sample output
4 0 5 9 -1 -1 0 2 8 -1 -1 0 7 4 -1 -1 0	16

SOLUTION

graphs – Floyd - Warsall

Algorithm analysis

In this problem you must implement the Floyd – Warshall algorithm. Instead of -1, we put a large positive integer in the cells of the input matrix. Then, in the matrix of shortest distances, find the largest number – it will be the maximum shortest distance.

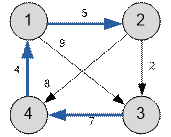
Example

Below given a graph from the statement. The maximum shortest distance is 16 and is achieved between vertices 3 and 2.

Algorithm realization

Store the adjacency matrix of the graph in array g. Plus infinity is assumed to be INF.

#define MAX 101

#define INF 10000000

int g[MAX][MAX];

Function floyd implements the Floyd – Warshall algorithm.

void floyd(void)

{

int i, j, k;

for(k = 0; k < n; k++)

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if (g[i][k] + g[k][j] < g[i][j]) g[i][j] = g[i][k] + g[k][j];

}

The main part of the program. Read the input graph, build the adjacency matrix g.

scanf("%d",&n);

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

{

scanf("%d",&g[i][j]);

if (g[i][j] < 0) g[i][j] = INF;

}

Run the Floyd – Warshall algorithm.

floyd();

In the variable res find the maximum shortest distance between the pairs of vertices.

for(i = 0; i < n; i++)

for(j = 0; j < n; j++)

if ((g[i][j] > res) && (g[i][j] < INF)) res = g[i][j];

Print the answer.

printf("%d\n",res);